Case Study: RPCA Anomaly Detection

One of the arbiters included with WARP is the RobustPcaArbiter.

This arbiter is based on an anomaly detection algorithm called Robust Principal Component Analysis. (RPCA). RPCA is a matrix decomposition algorithm that decomposes a measurement matrix M into the sum L + S + E. L is a low-rank matrix that represents the “normal” component of M. S is a sparse matrix that represents the anomalies in M, and E is an error term representing random noise.

RPCA has other applications besides anomaly detection. For example, it can be used to segment foreground/background in a surveillance video stream. L naturally corresponds to the static background, while S captures objects moving in the foreground. Similarly, RPCA can be used to remove specularities, shadows, or other irregular artifacts from photos as a preprocessing step to facial recognition; and to find irregular words as part of a spam detection or web indexing pipeline.

More detailed information can be found in the Candes09 and Zhou10 papers.

We use this arbiter internally to detect anomalies in recorded test measurements.

For example, a test suddenly running much slower may signify a performance regression that needs to be further investigated.

Background

In our internal legacy pipeline, test owners would set static thresholds on their tests for the purpose of detecting regressions due to degraded performance. This led to several problems:

• predicting the expected performance on production hardware is difficult a priori.
• updating thresholds over time puts onerous requirements on test owners.

We wanted to retain these threshold semantics because they are easy to reason about, but we wanted to remove the requirement of manual input from developers.

What if we could learn a suitable threshold, given the historic measurements for a test?

The SmartNumberArbiter combines the bisection method with RPCA to efficiently find the minimum measurement value that would be flagged as anomalous. This derived threshold is recorded as additional test metadata (using a tag), making the arbitration process easier to reason about than using a raw RobustPcaArbiter.

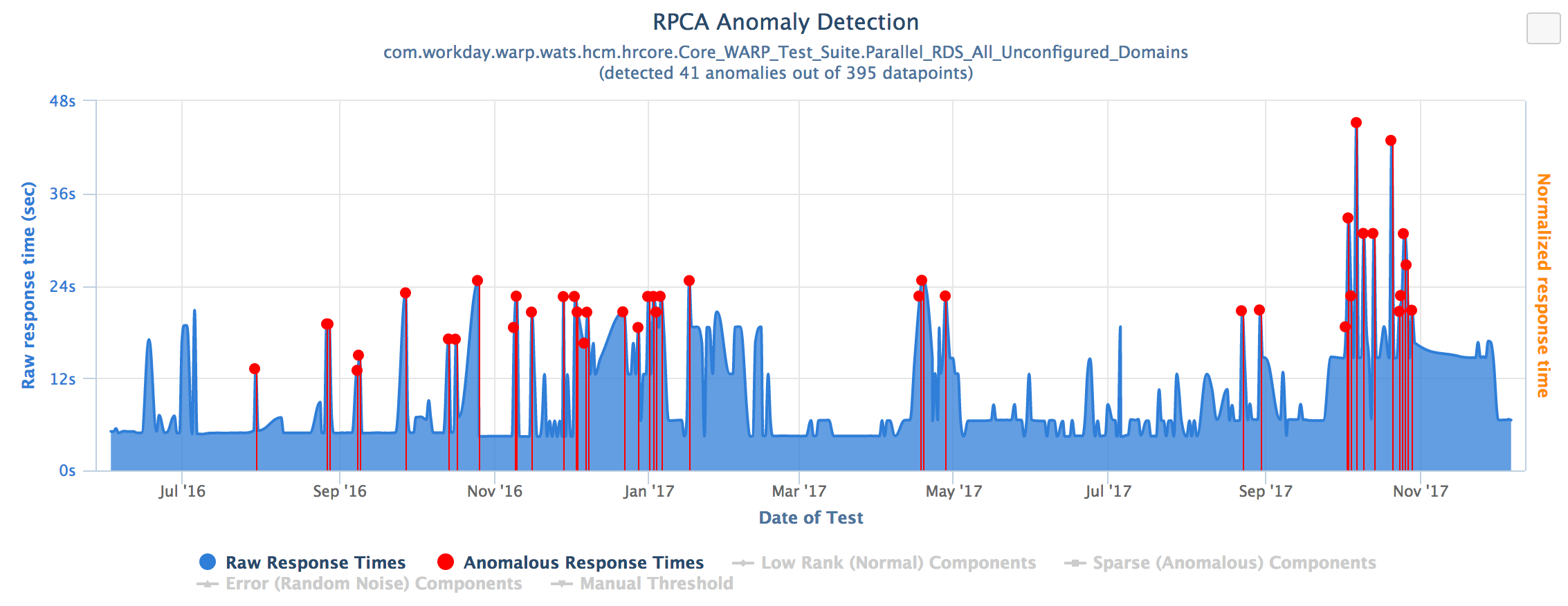
Internally, we use RPCA daily to detect anomalies in an online manner for test executions. This chart is taken from an internal dashboard and illustrates how the detected anomalies can look over time:

This code snippet illustrates how the RobustPcaArbiter can be used with an experiment:

1
2
3
4
5
6
7
8

@Test
def rpcaExample(): Unit = {
  using invocations 20 arbiters { 
    new RobustPcaArbiter 
  } measure { 
    someExperiment()
  }
}

Tuning

RPCA has several parameters that can be tuned for modifying the sensitivity of the algorithm. We use the defaults described in the Zhou10 paper as much as possible, however one parameter we encourage developers to experiment with is called tolerance factor. This is essentially a threshold in the normalized space of S, and directly controls how sensitive the algorithm is. Smaller values are more sensitive, while larger values give the algorithm more slack in determining whether a new test is anomalous. The tolerance factor is controlled via the property wd.warp.anomaly.rpca.s.threshold.

Double RPCA

However, one weakness of Robust PCA is that the system has a “short memory”. In other words, a sustained performance degradation will quickly be considered normal.

To remedy this, we developed a novel extension to RPCA called Double RPCA. This algorithm features an “extended training phase” where only past normal measurements are used to determine the current threshold value. One intuitive way to grasp the effects of this modification is to say that it, roughly speaking, “prevents Stockholm Syndrome”.

This variant is more strict with respect to sustained test performance degradation, and can lead to increased false positive rates over extended periods of time. This algorithm is a good fit for strictly judging the performance of some core functionality, especially code with constant-time asymptotic complexity. If the performance of a certain critical code block is never expected to change, Double RPCA is a good fit.